✍️ 周茂 , 陈箫翰  •  📅 2026-01-10

regress

官方文档:

regress

简介:

一维数据线性回归

regress 读取一个或多个表数据（也可从标准输入读取），确定每个分段最佳的线性[加权] 回归模型 \(y(x) = a + b x\) 。用户可自己指定输出哪些数据和模型。默认情况下，将 所有的输入数据作为一个整体来确定模型，但也可将数据分为等间距的数据段，在每段分别确定 模型。除了确定最贴近的模型外，该模块还可以输出所有可能的不同斜率的回归模型，这在分析 居于很多离群数据时非常有用。

备注

如果用户需要对 x 和 y 坐标的对数结果做拟合，可以使用 -iflags 选项在读数据后 将其转换为对数坐标

语法

gmt regress [ table ] [ -A[min/max/inc][+f[n|p]] ] [ -Clevel ] [ -Ex|y|o|r ] [ -Fflags ] [ -N1|2|r|w ] [ -S[r] ] [ -T[min/max/]inc[+i|n] |-Tfile|list ] [ -V[level] ] [ -W[w][x][y][r] ] [ -Z[+|-]limit ] [ -aflags ] [ -bibinary ] [ -bobinary ] [ -dnodata[+ccol] ] [ -eregexp ] [ -fflags ] [ -ggaps ] [ -hheaders ] [ -iflags ] [ -oflags ] [ -qflags ] [ -sflags ] [ -wflags ] [ --PAR=value ]

输入数据

table

一个或多个ASCII或二进制表数据。若不提供表数据，则会从标准输入中读取。

前两列为分别为 x 和 y。在设置 -W 和 -E 时，需要另外的 1-3 列作为数据的误差估计，或他们之间的相关系数（见 -W）。

可选选项

-A

-A[min/max/inc][+f[n|p]]

该选项有两个用法：

(1) 寻找回归的完整范围，而不是确定最佳拟合回归。以 inc 度为步长（默认 [-90/+90/1]），检查斜率角在 min 和 max 之间的所有可能回归线。 对于每个斜率，根据回归类型 -E 和不拟合范数 -N 设置来确定最佳截距。 对于每个数据分段，会在指定的角度范围内报告 angle 、 E 、 slope 、 intercept 这四列数据。 该范围内的最佳模型参数将写入分段头中，并在详细信息模式 ( -Vi ) 下报告。

(2) 除 -N2 外，附加 +f 以强制最佳回归仅考虑给定的受限角度范围 [默认考虑所有角度]。 可分别使用 +fn 或 +fp 表示负斜率或正斜率。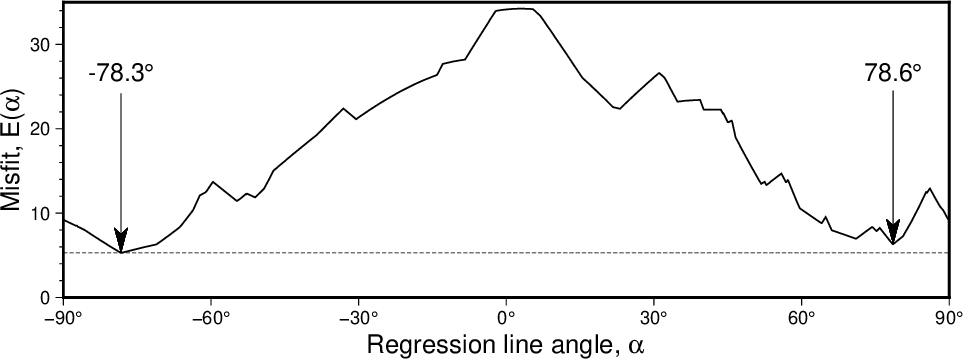

扫描斜率 -A 以观察使用 LMS ( -Nr ) 准则的完全正交回归的不拟合度量 (misfit) 随直线角度的变化情况。这里我们可以看到，最佳解对应的直线角度为 -78.3 度，但在 78.6 度处存在另一个几乎同样好的局部极小值。

-C

-Clevel

设置用于回归置信带 (confidence bands) 可选计算的置信水平（以 % 为单位）[默认为 95]。该选项仅在 -F 包含输出列 c 时使用。

-E

-Ex|y|o|r

线性回归类型，即选择应计算的不拟合 (misfit) 类型。可从以下选项中选择：

• x ： x 对 y 的回归，即不拟合是从数据点到回归线的水平方向测量。

• y ： y 对 x 的回归，即不拟合是从垂直方向测量 [默认]。

• o ：正交回归，即不拟合是从数据点到直线上最近点的正交距离测量。

• r ：缩减主轴回归 (Reduced Major Axis)，即不拟合是垂直和水平不拟合的乘积 [y]。

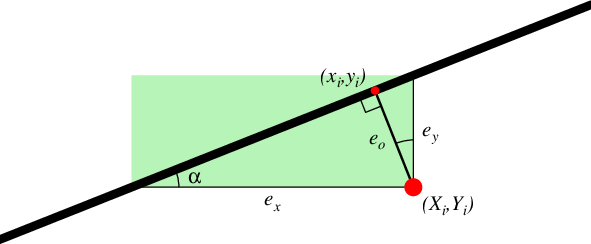
四种不拟合类型。对于 k = x, y 或 o，会最小化 \(e_k\) 长度的平方和。对于 -Er，则最小化绿色区域的面积之和。

-F

-Fflags

选择输出数据的列的组合，输出顺序将与指定的顺序一致。可从以下选项中选择：

• x ：观测值 x。

• y ：观测值 y。

• m ：模型预测值。

• r ：残差（残差 = 数据减去模型）。

• c ：回归的对称置信区间，参见 -C 以指定置信水平。

• z ：标准化残差或所谓的 z 分数 (z-scores)。

• w ：离群值权重（0 或 1）。对于 -Nw，这些是重新加权最小二乘法 (Reweighted Least Squares) 的权重。

默认值为 [xymrczw]。

使用 -Fp 会输出包含 12 个模型参数的单条记录:

npoints xmean ymean angle misfit slope intercept sigma_slope sigma_intercept r R n_effective

注意： R 只能在选择 -Ey 时设置。

-N

-N1|2|r|w

选择用于不拟合 (misfit) 计算的范数。可从以下选项中选择：

• 1 ： \(L_1\) 度量，绝对残差的平均值。

• 2 ：最小二乘法，平方残差的平均值 [默认值为 2]。

• r ：LMS，平方残差的最小中位数。

• w ：RLS，重新加权最小二乘法：在通过 LMS 识别并移除离群值后，计算平方残差的平均值。

传统回归使用 \(L_2\)，而 \(L_1\) 尤其是 LMS 在处理离群值时更为稳健。 如前所述，RLS 意味着先进行初始 LMS 回归，用其识别数据中的离群值并分配零权重，然后使用 \(L_2\) 范数重新进行回归。

-S

-S[r]

限制输出哪些记录。默认情况下，所有数据记录都将按照 -F 指定的格式输出。使用本选项排除被回归算法识别为离群值的数据点。 使用 -Sr 来反转此行为，仅输出离群值记录。

-T

-T[min/max/]inc[+i|n] |-Tfile|list

在参数指定的等间距点处评估最佳拟合回归模型。如果仅给出了 -Tinc，将把 min 和 max 重置为每个分段中 x 的极值。 若要完全跳过模型评估，使用 -T0。

-V

-V[level]

设置 verbose 等级 [w]。 (参数详细介绍)

-W

-W[w][x][y][r]

指定加权回归以及将要提供的权重类型。

• 如果提供了 x 观测值的 1-\(\sigma\) 不确定度，请附加 x 。

• 如果提供了 y 的 1-\(\sigma\) 不确定度，请附加 y 。

• 如果提供了 x 和 y 观测值之间的相关性，请附加 r。这些列在输入中出现的顺序应紧随必选的 x 和 y 列之后。

同时给出 x 和 y （以及可选的 r ）意味着进行正交回归。单独给出 x 需要配合使用 -Ex，单独给出 y 需要配合使用 -Ey 。

通过 \(w = 1/\sigma\) 的关系将 x 和 y 的不确定度转换为回归权重 w 。使用 -Ww 可以把输入列解释为预先计算好的权重。 注意 ：相对于回归线的残差将根据给定的权重进行缩放。大多数范数随后会对此加权残差进行平方（ -N1 是唯一的例外）。

-Z

-Z[±]limit

更改离群值检测的阈值：当使用 -Nw 时，残差 z 分数(z-scores)超过此 limit [默认 ±2.5] 的点将被标记为离群值。 若要仅将负或正的 z 分数视为可能的离群值，请指定带符号的 limit 。

-a

-a[[col=]name][,...]

控制输入或输出为 OGR/GMT 格式时对非空间元数据的处理方式。 (参数详细介绍)

-bi

-bi[ncols][type][w][+l|b]

控制二进制文件的输入格式。 (参数详细介绍)

-bo

-bo[ncols][type][w][+l|b]

控制二进制文件的输出格式。 (参数详细介绍)

-d

-d[i|o]nodata

将某些特定值当作 NaN。 (参数详细介绍)

-e

-e[~]"pattern" | -e[~]/regexp/[i]

筛选或剔除匹配指定模式的数据记录。 (参数详细介绍)

-f

-f[i|o]colinfo

显式指定当前输入或输出数据中每一列的数据类型。 (参数详细介绍)

-g

-g[a]x|y|d|X|Y|D|[col]zgap[+n|p]

确定数据或线段的间断。 (参数详细介绍)

-h

-h[i|o][n][+c][+d][+msegheader][+rremark][+ttitle]

在读/写数据时跳过文件开头的若干个记录。 (参数详细介绍)

-i

-icols[+l][+sscale][+ooffset][,...][,t[word]]

对输入的数据进行列选择以及简单的代数运算。 (参数详细介绍)

-o

-ocols[,...][,t[word]]

对输出的数据进行列选择以及简单的代数运算。 (参数详细介绍)

-q

-q[i|o][~]rows[+ccol][+a|f|s]

对输入或输出的行进行筛选，该选项在一定程度上可以代替 gawk 的某些功能。 (参数详细介绍)

-s

-s[cols][+a|+r]

设置 NaN 记录的处理方式。 (参数详细介绍)

-w

-wy|a|w|d|h|m|s|cperiod[/phase][+ccol]

将输入坐标转换为循环坐标。 (参数详细介绍)

-^ 或 -

显示简短的帮助信息，包括模块简介和基本语法信息（Windows下只能使用 -）

-+ 或 +

显示帮助信息，包括模块简介、基本语法以及模块特有选项的说明

-? 或无参数

显示完整的帮助信息，包括模块简介、基本语法以及所有选项的说明

--PAR=value

临时修改GMT参数的值，可重复多次使用。参数列表见 配置参数

ASCII 格式精度

ASCII 格式输出数据通过 gmt.conf 配置文件控制。控制经纬度格式的参数为 FORMAT_GEO_OUT ；控制绝对时间的的参数包括 FORMAT_DATE_OUT 和 FORMAT_CLOCK_OUT ；普通浮点数通过参数 FORMAT_FLOAT_OUT 控制。上述格式控制可能会导致精度损失，这会在下游计算中导致一些问题。 如果用户需要保证数据精度，则应考虑将数据写为二进制文件，或者使用 FORMAT_FLOAT_OUT 指定更多的有效数字。

生成一维数组

下面将展示如何使用 math 生成一维数组（其中大部分操作也可通过 linux 中的 seq 命令方便地实现）

不使用任何子选项

以 0.1 为步长，生成 3.1 到 4.2 等等间隔序列

gmt math -o0 -T3.1/4.2/0.1 T =
3.1
3.2
...
4.2

+a 选项

该选项不对生成的数列进行运算操作，而是将该数列以列的形式追加到输出表数据，类似 linux 中的 paste 命令。

+b 选项

以 3 和 20 分别为起点和终点，创建一个 2 的整数幂的列表，将生成 的整数幂以 1 为步长取值 -T3/20/1+b

gmt math -o0 -T3/20/1+b T =
4
8
16

+l 选项

以 7 和 135 分别为起点和终点，先创建一个 10 的整数幂的列表，当 inc 为 1 时，输出该列表；当 inc 为 2 时，同时输出该列表中每个元素的 1，2，5 倍值（不包括超出原始数据范围的部分）； 当 inc 为 3 时，同时输出 该列表中每个元素的 1，2，...，9 倍值（同样不包括超出原始数据范围的部分）。 -T7/135/2+l 将会生成如下数列

gmt math -o0 -T7/135/2+l T =
10
20
50
100

inc 为负整数时，将实现如下效果

gmt math -o0 -T1e-4/1e4/-2+l T =
0.0001
0.01
1
100
10000

+i 选项

该选项将以 1 作为默认步长，第三个数字做为每步长中的数字个数 length。假设需要在 1 分钟内每 24 秒生成一帧

gmt math -o0 -T0/60/24+i T =
0
0.0416666666667
0.0833333333333
0.125
0.166666666667
...
60

+n 选项

生成固定长度的数列。以 3.44 和 7.82 为 起点和终点，生成长度为 5 的等间隔序列

gmt math -o0 -T3.44/7.82/5+n T =
3.44
4.535
5.63
6.725
7.82

-T 后直接加文件或逗号分隔的数列

-T 后可以直接加文件，文件中即为要生成的列表；另外，可以直接使用逗号分隔， 将列表附加到 -T 选项后，如下为 Fibonacci 数列前 6 项

gmt math -o0 -T0,1,1,2,3,5 T =
0
1
1
2
3
5

注 ： 如果数列只包含一个值，必须在其后加逗号以表明仍是一个数列

+u 选项

如果文件或者逗号分隔的数列中有重复数字或未排序，可以使用 +u 选项去重并排序。

+t 选项

生成绝对时间序列。在 inc 后分别添加 y ，o ，d ，h ， m 和 s 表示时间步长的单位为年，月，日，时，分，秒。在其后附加 +t 选项， 可以进一步强调生成时间序列，也可以不加

gmt math -o0 -T2020-03-01T/2020-03-07T/1d T =
2020-03-01T00:00:00
2020-03-02T00:00:00
2020-03-03T00:00:00
2020-03-04T00:00:00
2020-03-05T00:00:00
2020-03-06T00:00:00
2020-03-07T00:00:00

生成距离序列

如果输入文件中包含两列以上的数据，可以使用前两列计算距离，并生成等距序列。 在 inc 后分别添加 d，m，s，e，f，M，n 和 u 表示距离步长的单位为度，分，秒，米，英尺，公里，英里，海里，英尺。如果 为笛卡尔坐标，使用 c 作为距离步长单位。

+e 选项

如果只给定 inc 而从数据中获取最大值和最小值，则 (max - min)/inc 可能 不是整数，GMT 讲会自动对 inc 进行一定的调整。如果不想调整 inc ，则可以 使用 +e 选项，GMT 会固定最小值，适当调整最大值。

注意事项

输出的分段头 (segment header) 将包含我们为每个分段计算的各种统计数据。 其顺序依次为： N （点数）、 x0 （加权平均值 x）、 y0 （加权平均值 y）、 angle （直线角度）、 E （不拟合度量）、 slope （斜率）、 intercept （截距）、 sigma_slope 以及 sigma_intercept 。 对于标准回归 ( -Ey )，还会报告皮尔逊相关系数 r 和判定系数 R 。最后以有效测量数 \(n_{eff}\) 结束。

对于加权数据，在计算需要最小化的平方回归不拟合度量 -N2 时，使用：

\[E_2(\nu) = \frac{\sum_{i=1}^n w_i e_i^2}{\sum_{i=1}^n w_i} \frac{n_{eff}}{n_{eff}-2},\]

其中有效测量数由下式给出：

\[n_{eff} = \frac{\left (\sum_{i=1}^n w_i\right )^2}{\sum_{i=1}^n w_i^2}.\]

因此 \(\nu = n_{eff} - 2\) 是有效自由度。

对于涉及除直线拟合之外更通用的线性模型回归，请参阅 math -A 以及 LSQFIT 或 SVDFIT 算子。

示例

返回通过远程文件 hertzsprung-russell.txt 中数据的最佳拟合正交回归线坐标:

gmt regress @hertzsprung-russell.txt -Eo -Fxm

对 points.txt 中的 x-y 数据进行标准最小二乘回归，并返回 x、y 以及带有 99% 置信区间的模型预测值:

gmt regress points.txt -Fxymc -C99 > points_regressed.txt

若只想获取上述回归的斜率:

slope=`gmt regress points.txt -Fp -o5`

对数据 rough.txt 进行重新加权最小二乘回归，并返回 x、y、模型预测值以及 RLS 权重:

gmt regress rough.txt -Fxymw > points_regressed.txt

对数据 crazy.txt 进行正交最小二乘回归，但先对 x 和 y 取对数，然后返回 x、y、模型预测值和标准化残差 (z-scores):

gmt regress crazy.txt -Eo -Fxymz -i0-1l > points_regressed.txt

对于同一文件，检查正交 LMS 不拟合度量在 0 到 90 度之间（步长 0.2 度）如何随角度变化:

gmt regress points.txt -A0/90/0.2 -Eo -Nr > points_analysis.txt

强制正交 LMS 选择具有正斜率的最佳解:

gmt regress points.txt -A+fp -Eo -Nr > best_pos_slope.txt

参考文献

Bevington, P. R., 1969, Data reduction and error analysis for the physical sciences, 336 pp., McGraw-Hill, New York.

Draper, N. R., and H. Smith, 1998, Applied regression analysis, 3rd ed., 736 pp., John Wiley and Sons, New York.

Rousseeuw, P. J., and A. M. Leroy, 1987, Robust regression and outlier detection, 329 pp., John Wiley and Sons, New York.

York, D., N. M. Evensen, M. L. Martinez, and J. De Basebe Delgado, 2004, Unified equations for the slope, intercept, and standard errors of the best straight line, Am. J. Phys., 72(3), 367-375.

相关模块

math, trend1d, trend2d