grdflexure

贡献者:

周茂

最近更新日期:

2024-06-07

官方文档:

grdflexure

简介:

计算 3-D 载荷在多种流变学条件下产生的挠曲变形

目前均衡研究中主要存在 3 种模型，分别为 Pratt 模型，Airy 模型以及挠曲模型。 grdflexure 即为挠曲均衡模型，其可计算地形载荷 \(h(\mathbf{x})\) 在 5 种不同流变学条件下引起的变形，所有情况中承载地形的板（通常为地壳或者岩石圈） 的厚度都认为是相同的，以下为 5 种流变基础：

  1. 弹性板覆盖在无粘性的半空间上

  2. 弹性板覆盖在粘性板上（Firmoviscous 或者 Kelvin-Voigt）

  3. 弹性板覆盖在粘性层上，然后整体覆盖在粘性半空间上

  4. 粘弹性板覆盖在无粘性半空间上

  5. 线性粘弹性模型，弹性板覆盖在无粘性半空间上，已知初始和结束时的弹性板厚度

五种流变基础分别对应均衡研究中对岩石圈/地壳的五种假设，其对应的响应函数分别为 elastic [1; \(\Phi_e(\mathbf{k})\)]， firmoviscous [2,3; \(\Phi_{fv}(\mathbf{k},t)\)]， viscoelastic [4; \(\Phi_{ve}(\mathbf{k},t)\)]， 和 general linear (viscoelastic) [5; \(\Phi_{gl}(\mathbf{k},t)\)]。如果 （粘）弹性板消失（厚度为 0），则退化为 Airy 均衡模型（1,4）或者纯粘性模型（2，3）。 还可为模型提供等间隔的网格以研究随时间变化的结果；此外还可为模型制定相关的流体 基础和常数，包括板内应力。

语法

gmt grdflexure input -Drm/rl[/ri]/rw[+rrr] -E[Te[k][/Te2[k]]] -Goutgrid [ -ANx/Ny/Nxy ] [ -Cp|yvalue ] [ -Fnu_a[/h_a[k]/nu_m] ] [ -Hrhogrid [ -Llist ] [ -Mtm ] [ -Nparams ] [ -Q ] [ -Sbeta ] [ -Tt0[/t1/dt[+l]]|file ] [ -V[level] ] [ -Wwd][k] [ -Zzm][k] [ -hheaders ] [ -fflags ] [ --PAR=value ]

必选选项

topogrd

地形网格载荷，可以为多种形式：

  • 单个二维二进制网格文件，单位为 m

  • 如果使用 -T 选项，topogrd 可以是一个 C 语言语法形式的模版名，见 网格文件名模版 。将为每个时间加载不同的地形网格。 因此，加载时间必须与 -T 给出的时间一致（但并非所有的时间都需要对应的文件）。

  • 可以将 topogrd 指定为 flist+l ，其中 flist 为文本文件， 其中每条记录均包含一个 topogrd 文件名和对应的加载时间（例如 grdseamount 的 -M 选项生成的列表）。加载的时间可以和 -T 给出的时间不同，参见 -T 。注 ：如果 flist 文件中包含第三列， 则第二列为加载地形的密度，此密度可以覆盖 -D 选项设置的固定密度 rl 。 最后一列为格式化的你那呆字符串。

  • 一个以 “.lis” 为后缀的文本文件，该后缀会自动被识别为文件列表，而不需要 +l 选项。

注 ： 水平方向维度输入单位应该为米。如果输入网格单位为 km，则可以追加 +uk ，在程序内部会将 km 转换为 m。所有的文件都需要包含相同的维度，如果 文件中存在 NaN，则会自动被替换为 0，使用 -V 选项可查看这些替换报告。

-Drm/rl[/ri]/rw[+rrr]

分别设置地幔，载荷，填充物和水（或空气）的密度。如果 ri 和 rl 不同， 则确定一个近似解。如果 ri 没有指定，则默认其等于 rl 。密度的单位可以是 km/m^3 或 g/cm^3 。 注 ： 如果使用 -H 选项指定可变密度的负载，则 rl 必须设置为 -。 无论载荷的密度是否可变，都可以通过 +r 指定一个固定的根部密度，即载荷 下方的填充密度。这会强制根据 rl/rr 的比例重新调整载荷地形，然后将 rl 重置 为 rr 以计算形变。

-E[Te[k][/Te2[k]]

设置弹性板厚度（单位为 m）, k 表示单位为 km。如果弹性板厚度的值超过 了 1e10，认为该值超过岩石圈有效弹性厚度的实际范围，GMT 将其认为是抗挠刚度 ，而不是弹性板厚度 D （默认情况下 D 由有效弹性厚度 Te ，杨氏模量 和泊松比计算，见 -C 参数）。如果 -E 后不加任何参数且和 -F 同时使用，则表明不设置弹性板，GMT 将返回带有软流圈或者不含软流圈的纯粘性 响应。通过给定初始的弹性厚度 Te 和最终弹性厚度 Te2 , 可以选择设置为 线性粘弹性响应，这时需要同时使用 -M 选项。

-Goutgrid[=ID][+ddivisor][+ninvalid] [+ooffset|a][+sscale|a] [:driver[dataType][+coptions]]

输出网格文件名，其中各子选项的含义见 网格文件 如果使用 -T 选项，则需要使用 C 语言的语法指定输出格网序列的名称格式。 见 网格文件名模版 。 如果输出文件名中包含 %s (单位名称) 或 %c (单位字母)，GMT 将会使用每个 网格对应的时间生成文件名，否则会使用年作为时间生成文件名。

可选选项

-ANx/Ny/Nxy

指定 x 和 y 方向的压力或者拉力以及任意剪应力。压力用负值表示，拉力用 正值表示，由于 N 为深度积分的水平应力，所以单位为 Pa·m。

-Cp|yvalue

分别使用 p 和 y 修改泊松比的默认值 [0.25] 和杨氏模量的默认值 [7.0e10 N/m^2]

-Fnu_a[/h_a[k]/nu_m]

使用刚粘性模型，并通过 -E 指定弹性板厚度。可以指定弹性板覆盖的粘性 半空间的粘度 nu_a ，也可以追加软流圈的厚度 h_a 以及下地幔的粘度 nu_m ，这种情况下，nu_a 即变为软流圈的粘度。粘度单位为 Pa.s。软 流圈厚度单位默认为 m，追加 k 可变为 km。该选项不能与 -M 选项 同时使用。

-Hrhogrid

指定可变密度的载荷网格。可以为单个网格或者网格文件模版（见 网格文件名模版 ）。使用该选项需要在 -D 选项中设置 rho_l 为 -。注 ：如果该模块输入的载荷网格是一个网格列表，则密度网格 必须同时在输入的网格列表中给出，而不是使用这里的 -H 选项给出。

-Llist

将所有创建的网格的名称和对应的时间写入到 list 文件中。该选项需要 -T 选项。文本文件的第一列为以年为单位的时间，最后一列则为格式化的 时间，因此，输出的文本文件的格式为 time flexuregrid timetag 。

-N[a|f|m|r|s|nx/ny][+a|d|h|l][+e|n|m][+twidth][+v][+w[suffix]][+z[p]]

选择或查询适合 FFT 的网格尺寸并设置可选参数。 FFT 维度选取：

-Na 以得到最准确的结果来选择 FFT 的维度

-Nf 将 FFT 维度设置为数据实际长度

-Nm 以最小的运行内存来选择 FFT 的维度

-Nr 以最快的计算速度来选择 FFT 的维度

-Ns 列出所有可选的维度，然后退出

-Nnx/ny 将会设置 FFT 的维度为 nx 和 ny （维度必须大于等于网格范围）。 默认情况下，-N 同样会选择大于网格范围的维度，在此情况下会对 FFT 的速度和精度 进行优化。如果 FFT 的维度大于网格的范围，对网格进行扩展并 taper（两端尖灭）到 0。

设置移去数据的趋势：

+d: 移去趋势，即去除符合程度最好的线性趋势 [默认]

+a: 移去均值

+h: 移去中值，即 0.5 * (max + min).

+l: 不做任何处理

为避免边缘效应，设置对数据边界的处理：

+e 在数据边界使用边界点对称来扩展网格 [默认]

+m 在数据边界使用镜像对称来扩展数据

+n 不使用任何数据扩展

+t 从数据的边界到 FFT 网格边界使用 taper 使数据趋近于 0 [100%]。 使用 +twidth 可以修改扩展的范围。当设置了 +n 选项时，不进行数据扩展， 且将 taper 用于数据内部，而不是扩展的范围。 （译注：100% 的含义为在网格四周分别扩展数据范围的 50%，然后使用 taper 来填充新扩展 的区域。Taper 或可译为两端尖灭，是一种加窗方法，且窗为平顶，这里默认使用的 cos 函数形状，即 Tukey 窗。将数据边界上的值逐渐减小到 0 ，以避免谱泄漏 ）

+v 在处理中报告适合的维度

中间结果的设置，用来保存中间结果，以便用户可以使用中间结果自行进行某步骤：

+w[suffix] 设置去趋势/数据扩展/taper 的网格后缀， 即最终生成 xxx_suffix.ext 的结果。

+z 可用来保存执行 FFT 后的复数结果，包括两个网格，文件名将为 xxx_real.ext 和 xxx_imag.ext。追加 p 可以设置为 polar 形式，即幅度和相位，文件名为 xxx_mag.ext 和 xxx_phase.ext 。

-Mtm

使用粘弹性模型，并通过 -E 选项设置弹性板的厚度。可追加粘弹性模型 的 Maxwell 时间 tm ，单位为年，追加 k 选项表示 kyr ，追加 M 表示 Myr。该选项不能和 -F 选项同时使用。

-Q

不计算形变，而是在选定的参数下计算响应函数，见下面的 响应函数理论

-Sbeta

指定一个指数，该指数反映了载荷导致的形变在四周连带形成的凹陷（常称为 “护城河”）中的物质的密度。若该指数为 1，则表示护城河完全填充了密度为 ri 的物质（即护城河完全被其他物质填充），若为 0，则表示完全填充了 密度为 rw 的物质（即没有填充物，被水填充），默认为 1。

-Tt0[/t1/dt[+l]]|file

指定起始时间 t0 ，终止时间 t1 以及时间间隔 dt [默认只进行一次 与时间无关的计算]。对于单个时间， 只需指定 t0 。默认单位为年，追加 k 表示 kyr，M 表示 Myr。 使用 +l 选项以及将 dt 替换为 n 可以设置对数时间轴。或者，还 可以设置一个文件 file ，文件中第一列为时间，其中的时间也可追加单位， 不追加时默认使用年。对于其中的每个时间点，该模块都输出一个网格，见 -G 和 网格文件名模版 。

-Wwd[k]

指定水深，单位为 m，追加 k 表示 km。必须为正值，默认为 0。如果 载荷超过该深度，则对水面上的部分进行缩放以补偿水和空气的密度差异。

-Zzm[k]

指定挠曲变形的参考深度 zm （即 Moho 面），单位为 m，追加 k 表示单位为 km，必须为正值，默认值为 0。在输出前将在挠曲变形上减去 该值。因此，如果观测水平面位于海平面，如需观测 5km 深处的海底形变， 则使用-Z5k，输出未变形面的 z = -5000。

-V[level] (more …)

设置 verbose 等级 [w]

-fflags

地理坐标网格将会被转换为平地球下的米，其中使用椭球参数近似

-^ 或 -

显示简短的帮助信息，包括模块简介和基本语法信息（Windows下只能使用 -）

-+ 或 +

显示帮助信息，包括模块简介、基本语法以及模块特有选项的说明

-? 或无参数

显示完整的帮助信息，包括模块简介、基本语法以及所有选项的说明

--PAR=value

临时修改GMT参数的值，可重复多次使用。参数列表见 配置参数

网格文件名模版

网格文件名允许使用一定的规则来定制模版：

  • 若将格式化的时间作为文件名的一部分，则使用单个 %s 作为模版的一部分 （例如，smt_%s.grd）

  • 若想控制名称中数字的格式，但仍保留时间的单位，则可以使用 %f 和 %c 的组合。例如：smt_%05.1f%c.grd 将会生成类似 smt_001.1M.grd 的文件名。 时间将会进行缩放以适应设置的单位

  • 如果不想使用任何单位，则只需给定一个浮点格式的模版，例如： smt_%05.1f_name.grd。时间的单位与原单位相同，即不使用缩放。

详细的格式信息，见 C 语言 printf 语法。

网格距离单位

如果输入的笛卡尔网格的水平方向距离的单位不是米，可以通过对输入文件名 +uunit 来将指定的单位转换为米。例如：对输入文件 +uk 将会把 输入网格的 x 和 y 坐标的单位从 km 转换为 m。如果输入网格为地理网格，可以 通过 -fflags 将单位转换为米。

注意事项

本模块使用矩形笛卡尔 FFT 计算。如果用户计算区域接近极点，则应该考虑使用笛卡尔 坐标；从地理坐标到笛卡尔坐标的转换可以使用 grdproject 模块实现。

示例

接下来使用高斯海山来演示 grdflexure 的使用。

  1. 在位置 (300,300) 存在一个半径为 50 km，高度为 5000 m 的平顶海山，使用 grdseamount 可以生成该海山网格文件

    echo 300 300 0  40  40  5000 | gmt grdseamount -R0/600/0/600+uk -I1000 -Gsmt.nc t.txt -Dk -E -F0.1 -Cg

  2. 以该海山 smt.nc 作为载荷，计算弹性形变，假定弹性板厚度为 10 km

    gmt grdflexure smt.nc -Gflex.nc -E10k -D2700/3300/1035

  3. 使用 -A 可以计算平面内应力对结果的影响

    gmt grdflexure smt.nc -Gflex.nc -E10k -D2700/3300/1035 -A-4e11/2e11/-1e12

  4. 假定流变基础不为纯弹性，而是为粘弹性，计算该海山在 20 km 厚板上产生的形变， 密度为默认为常用的值，Maxwell 时间设置为 40 kyr

    gmt grdflexure smt.nc -Gflex.nc -E20k -D2700/3300/1035 -M40k

  5. 假定流变基础为刚粘性，板厚度为 15 km，密度仍与上例相同，粘性地幔粘度为 2e21，计算 在此条件下海山造成的形变

    gmt grdflexure smt.nc -Gflex.nc -E15k -D2700/3300/1035 -F2e21

  6. 假定流变基础为线性粘弹性，Maxwell 时间为 100 kyr，初始有效弹性厚度为 40 km， 结束时有效弹性厚度为 15 km，计算海山造成的形变

    gmt grdflexure smt.nc -Gflex.nc -E40k/15k -D2700/3300/1035 -M100k

基于指定的流变基础，计算刚粘性响应函数:

gmt grdflexure -D3300/2800/2800/1000 -Q -F2e20

指定流变学基础，由 l.lis 指定一系列时间和响应的载荷，计算器刚粘性响应。 其中时间间隔为 1 Ma

gmt grdflexure -T1M =l.lis -D3300/2800/2800/1000 -E5k -Gflx/smt_fv_%03.1f_%s.nc -F2e20 -Nf+a

转换函数

如果使用 -Q 选项，则不计算挠曲变形，也不需要输入文件，而是输出转换函数。 转换函数 \(\Phi(\mathbf{k},t)\) 将被存入 7 个文件，分别对应 7 个不同的 有效弹性厚度（1，2，5，10，20，50 以及 100 km）。每个文件的前两列为以 km 为单位的波长以及以 1/m 为单位的波数，波长的范围和间隔为 1:1:3000 km。每个 文件都计算了多个加载时间的转换函数，包括 1，2，5，10，20，50，100，200 k 年 以及 1 和 2M 年。对于纯弹性响应函数，则并不输出所有上述加载时间的结果，而是 只输出一个结果。这 7 个文件命名为 grdflexure_transfer_function_te_te_km.txt， 其中 te 将被替换为有效弹性厚度值。

响应函数理论

由地形 \(h(\mathbf{x})\) 引起的变形 \(w(\mathbf{x})\) 随时间的变化在傅立叶域（波数域） 中可由下式得到：

\[W(\mathbf{k},t) = \gamma \left (\frac{\rho_l - \rho_w}{\rho_m - \rho_l} \right ) H(\mathbf{k}) \Phi(\mathbf{k},t) = \gamma A H(\mathbf{k}) \Phi(\mathbf{k},t)\]

式中，\(\mathbf{k} = (k_x, k_y)\) 为波数向量，\(k_r\) 为其幅值，\(H(\mathbf{k})\) 为波数域中的地形载荷，即 \(h(\mathbf{x})\) 的傅立叶变换，\(A\) 为 Airy 密度比， \(\gamma\) 常数，取决于填充物密度，\(\Phi(\mathbf{k},t)\) 为所选流体基础的响应函数。 grdflexure 读取一个或者多个载荷 \(h(\mathbf{x})\) ，将其转换为 \(H(\mathbf{k})\) ， 计算响应函数，并计算最终的变形 \(W(\mathbf{k},t)\) ，经过 IFFT 后即得到一个或者多个载荷 引起的形变 \(w(\mathbf{x})\) 。

可变加载密度

如果负载密度是可变的，即使用 -H 选项设置输入网格，则简单地将加载的高度调整为和平均加载密度等效的高度； 即满足 \(\rho_l(\mathbf{x})\cdot h(\mathbf{x}) = \bar{\rho_l}\cdot h'(\mathbf{x})\) 。

水下和水上加载

如果使用 -W 指定水深，则会检查负载的高度（或者如上述 可变加载密度 中的调整后的高度）是否超过水深。 如果超过，则将高于水面的的负载高度调整以适应密度差的变化（即，原本水与负载之间的密度差变为空气与负载 之间的密度差，因此需调整对应的高度）；因此，水上部分的高度将乘以 :math:`frac{rho_l}{rho_l - rho_w} 。

填充物密度

如果 \(\rho_i = \rho_l\) ，则 \(\gamma = 1\) ，如果填充物的密度随空间变化，则无法 使用 FFT 求解。通过使 \(\rho_l = \rho_i\) 以及下面的公式可以避免这种情况：

\[\gamma = \sqrt{\frac{\rho_m - \rho_i}{\rho_m - \rho_l}}\]

这种近似在除板上负载非常大的情况下表现都很好（Wessel, 2001）。

Source Code

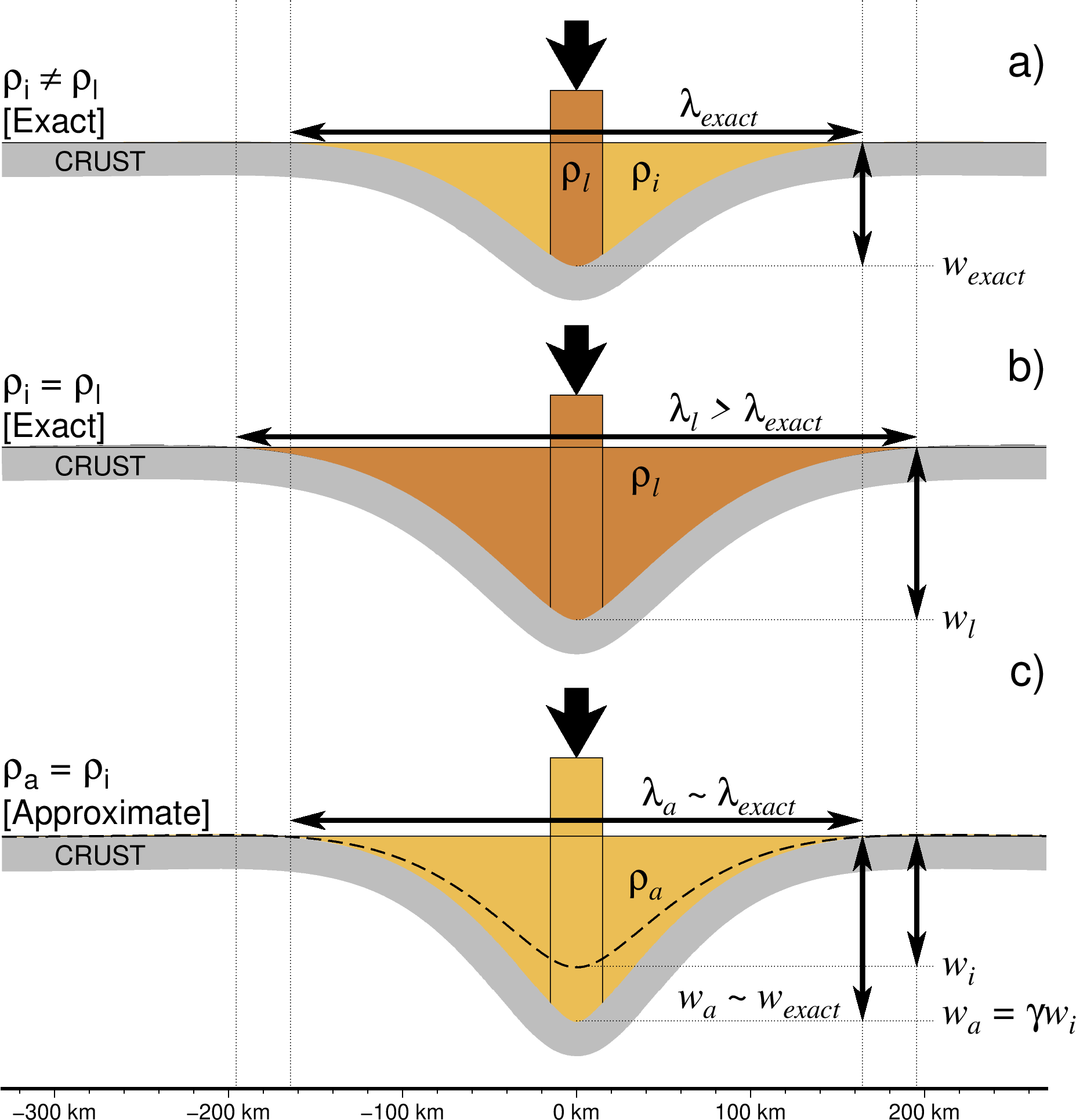
../../_images/8e36e209d696ab19a10f12cf775de338.png

上图从 Wessel(2016) 中修改得到， (a) 图中护城河中物质的密度（ \(\rho_i\) ）以及负载的密度（\(\rho_l\)）不同。 不幸的是，FFT 解需要一个常数密度差异。 (b) 图中使用负载密度作为填充物密度，这种情况会高估形变的波长（\(\lambda_l\)）以及幅度 （\(w_l\)）。 (c) 图中使用填充物密度作为负载密度，计算结果中形变的波长大致正确，但低估了七幅度（虚线）。 我们通过对 \(w_i\) 缩放 \(\gamma\) 可以得到满意的结果。

弹性响应函数

与时间无关的弹性响应函数为

\[\Phi_e(\mathbf{k}) = \left [ 1 + \alpha_r^4 + \epsilon_x \alpha_x^2 + \epsilon_y \alpha_y^2 + \epsilon_{xy} \alpha_{xy}^2 \right ]^{-1}, \quad \alpha_s = k_s / k\]

其中 k 为形变波数，\(\epsilon_s\) 为常数，\(N_x, N_y, N_{xy}\) 为下标 \(s = \left (x, y, xy \right )\) 的平面应力。

\[k = \left [ \frac{(\rho_m - \rho_i)g}{D} \right ]^{\frac{1}{4}}, \quad \epsilon_s = \left [ \frac{N_s}{(\rho_m - \rho_i)g} \right ]^{\frac{1}{2}}\]

在常见的情况下，\(N_s\) 都是 0，并且弹性响应函数具有各向同性：

\[\Phi_e(k_r) = \left [ 1 + \alpha_r^4 \right ]^{-1}\]

刚粘性响应函数

刚粘性响应函数 \(\Phi(\mathbf{k},t)\) 在给定的波数和时间下缩放形变信息，并受 流变基础参数以及平面应力的影响：

\[\Phi_{fv}(\mathbf{k},t) = \Phi_e(\mathbf{k}) \left [ 1 - \exp \left \{ - \frac{(\rho_m - \rho_l) \tau(k_r)}{\rho_m\Phi_e(\mathbf{k})} t \right \} \right ]\]

如果流变基础为非粘性半空间，则 relaxation parameter \(\tau(k_r) = \infty\) 与时间无关，且 \(\Phi_{fv}(\mathbf{k},t) = \Phi_e(\mathbf{k})\) 。否则：

\[\tau(k_r) = \frac{\rho_m g}{2 \eta_m k_r} \beta(k_r)\]

式中，\(\beta(k_r)\) 取决于是否在粘性（\(\beta(k_r) = 1\)）半空间上添加一个 有效弹性厚度为 \(T_a\) 粘度为 \(\eta_a\) 的层(Cathles, 1975; Nakada, 1986)。 如果不存在该层，则 \(\beta(k_r) = 1\) ，否则：

\[\beta(k_r) = \frac{(\theta + \theta^{-1}) CS + k_r T_a (\theta - \theta^{-1}) + S^2 + C^2}{2CS\theta + (1-\theta)k_r^2 T_a^2 + \theta S^2 + C^2}\]

式中

\[\theta = \eta_a/\eta_m, \quad S = \sinh (k_r T_a), \quad C = \cosh (k_r T_a)\]

Airy 和粘性响应函数

在极限的情况下 \(t \rightarrow \infty, \tau \rightarrow 0\) ，即得到一个纯 弹性解：

\[W(\mathbf{k}) = A \gamma H(\mathbf{k}) \Phi_e(\mathbf{k})\]

否则，如果该弹性板刚度为 0 （-E0），则 \(\Phi_e(\mathbf{k}) = 1\) 且 响应函数为纯粘性并是各向同性的：

\[\Phi_v(k_r,t) = \left [ 1 - \exp \left \{ - \frac{(\rho_m - \rho_l) \tau(k_r)}{\rho_m} t \right \} \right ]\]

对于 \(t \rightarrow \infty\) （或一个非粘性的半空间），则得到 Airy 均衡 \(w(\mathbf{x}) = A h(\mathbf{x})\) 。

Maxwell 粘弹性响应函数

对于第四种流变基础，粘弹性响应函数为（仅适用于无粘性基础）

\[\Phi_{ve}(\mathbf{k},t) = 1 - \left [ 1 - \Phi_e(\mathbf{k}) \right ] \exp \left \{ - \frac{t}{t_m} \Phi_e(\mathbf{k}) \right \}\]

式中 \(t_m\) 为 Maxwell relaxation time(Watts, 2001)。

线性粘弹性响应函数

对于第五种流变基础，线性粘弹性响应函数为（仅适用于无粘性基础）(Karner, 1982)：

\[\Phi_{gl}(\mathbf{k},t) = \Phi_f(\mathbf{k}) + \left [ \Phi_i(\mathbf{k}) - \Phi_f(\mathbf{k}) \right ] \exp \left \{ - \frac{t}{t_m} \frac{D_i \Phi_i(\mathbf{k})}{D_f \Phi_f(\mathbf{k})} \right \}\]

下标 i 和 f 分别指起始时间（t = 0）以及终止时间（\(t = \infty\)）， 刚度相关的参数为 \(D_i, D_f\) ， 弹性响应函数为 \(\Phi_i, \Phi_f\) 。

参考文献

Cathles, L. M., 1975, The viscosity of the earth’s mantle, Princeton University Press.

Karner, G. D., 1982, Spectral representation of isostatic models, BMR J. Australian Geology & Geophysics, 7, 55-62.

Nakada, M., 1986, Holocene sea levels in oceanic islands: Implications for the rheological structure of the Earth’s mantle, Tectonophysics, 121, 263–276, https://doi.org/10.1016/0040-1951(86)90047-8.

Watts, A. B., 2001, Isostasy and Flexure of the Lithosphere, 458 pp., Cambridge University Press.

Wessel. P., 2001, Global distribution of seamounts inferred from gridded Geosat/ERS-1 altimetry, J. Geophys. Res., 106(B9), 19,431-19,441, https://doi.org/10.1029/2000JB000083.

Wessel, P., 2016, Regional–residual separation of bathymetry and revised estimates of Hawaii plume flux, Geophys. J. Int., 204(2), 932-947, https://doi.org/10.1093/gji/ggv472.

相关模块

gmtflexure, grdfft, gravfft, grdmath, grdseamount